1. 树状数组是什么？为什么需要它？

想象一个场景：你有一个数组 a，需要频繁地做两件事：

  1. 修改数组中某个元素的值。
  2. 查询数组中任意一个区间的和（例如，从索引 l 到 r 的所有元素之和）。

我们可以用一些朴素的方法来解决：

  • 普通数组：
    • 修改元素：O(1)，非常快。
    • 查询区间和：O(n)，需要遍历区间，如果查询次数很多，会非常慢。
  • 前缀和数组：
    • 我们预处理一个 preSum 数组，preSum[i] = a[1] + ... + a[i]。
    • 查询区间和 [l, r]：O(1)，只需计算 preSum[r] - preSum[l-1]，非常快。
    • 修改元素 a[i]：O(n)，因为 a[i] 的改变会影响到 preSum[i] 及之后的所有元素，你需要更新 preSum[i], preSum[i+1], ..., preSum[n]，非常慢。

可以看到，这两种方法在“修改”和“查询”上都有一个操作是 O(n) 的，无法同时做到高效。

树状数组 (Fenwick Tree) 就是为了解决这个问题而生的。它是一种巧妙的数据结构，可以在 O(log n) 的时间复杂度内完成 单点更新 和 前缀和查询。这使得它在需要频繁进行这两种操作的问题中非常高效。

2. 核心思想与原理

树状数组的核心思想是：用一个辅助数组 t，让 t[i] 存储原数组 a 中一个特定区间的和。这个“特定区间”的划分非常精妙，它使得更新和查询都能以类似二分的方式沿着一条“树链”进行，从而保证了 O(log n) 的复杂度。

lowbit 函数

lowbit(x) 是理解树状数组的关键。它的功能是获取 x 的二进制表示中，最低位的那个 ‘1’ 以及它后面的所有 ‘0’ 构成的数值。

例如：

  • x = 6，二进制是 0110。最低位的 ‘1’ 在第二位，所以 lowbit(6) 的结果是 0010，即十进制的 2。
  • x = 7，二进制是 0111。最低位的 ‘1’ 在第一位，所以 lowbit(7) 的结果是 0001，即十进制的 1。
  • x = 8，二进制是 1000。最低位的 ‘1’ 在第四位，所以 lowbit(8) 的结果是 1000，即十进制的 8。

如何计算 lowbit(x)？
一个非常简洁的位运算技巧：lowbit(x) = x & (-x)。
（在计算机中，负数以补码形式存储，-x 等于 ~x + 1，这个位运算 x & (~x + 1) 恰好能得到上述结果）。

树状结构

lowbit(x) 定义了 t[x] 所管理的区间长度。具体来说，t[x] 存储的是原数组 a 中 (x - lowbit(x), x] 这个长度为 lowbit(x) 的区间的和。

我们以一个大小为 8 的数组为例：

  • t[1]: lowbit(1)=1. 区间是 (1-1, 1] = (0, 1]. 存储 a[1].
  • t[2]: lowbit(2)=2. 区间是 (2-2, 2] = (0, 2]. 存储 a[1] + a[2].
  • t[3]: lowbit(3)=1. 区间是 (3-1, 3] = (2, 3]. 存储 a[3].
  • t[4]: lowbit(4)=4. 区间是 (4-4, 4] = (0, 4]. 存储 a[1] + a[2] + a[3] + a[4].
  • t[5]: lowbit(5)=1. 区间是 (5-1, 5] = (4, 5]. 存储 a[5].
  • t[6]: lowbit(6)=2. 区间是 (6-2, 6] = (4, 6]. 存储 a[5] + a[6].
  • t[7]: lowbit(7)=1. 区间是 (7-1, 7] = (6, 7]. 存储 a[7].
  • t[8]: lowbit(8)=8. 区间是 (8-8, 8] = (0, 8]. 存储 a[1] + ... + a[8].

我们可以画出这个结构图，它看起来像一棵树：

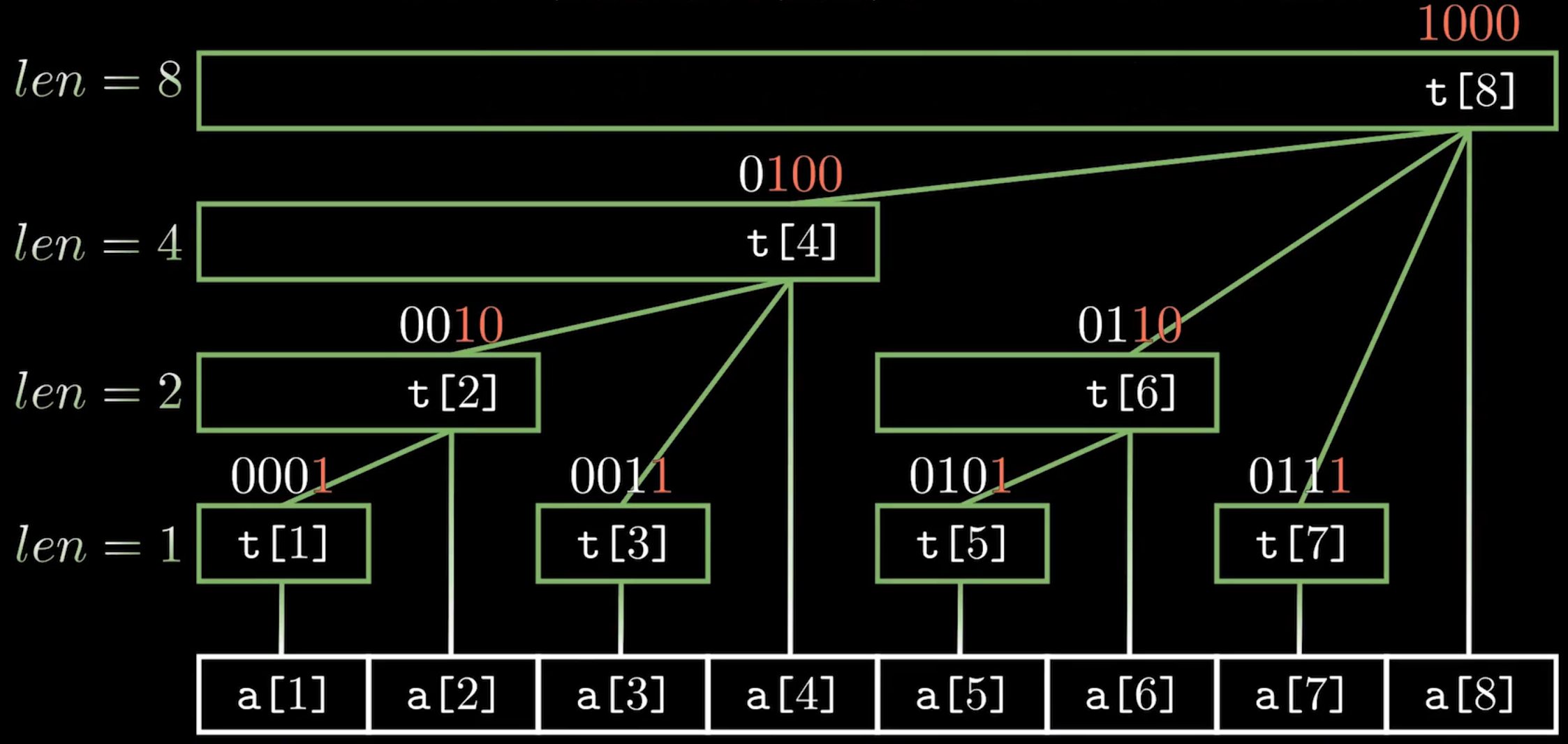
树状数组结构图

这张图清晰地展示了 t[i] 的依赖关系。

通过观察我们可以发现t[x]节点覆盖的长度就是lowbit(x)，并且t[x]节点的父节点为t[x + lowbit(x)]，整棵树的深度为logn + 1，n表示原数组的长度

单点更新 (update(index, delta))

当你修改原数组 a[i] 的值（增加 delta）时，你需要更新所有管辖范围包含 a[i] 的 t 数组元素。

这些需要被更新的 t 元素形成了一条向上的路径。如何找到下一个要更新的节点（父节点）？
规律是：i = i + lowbit(i)。

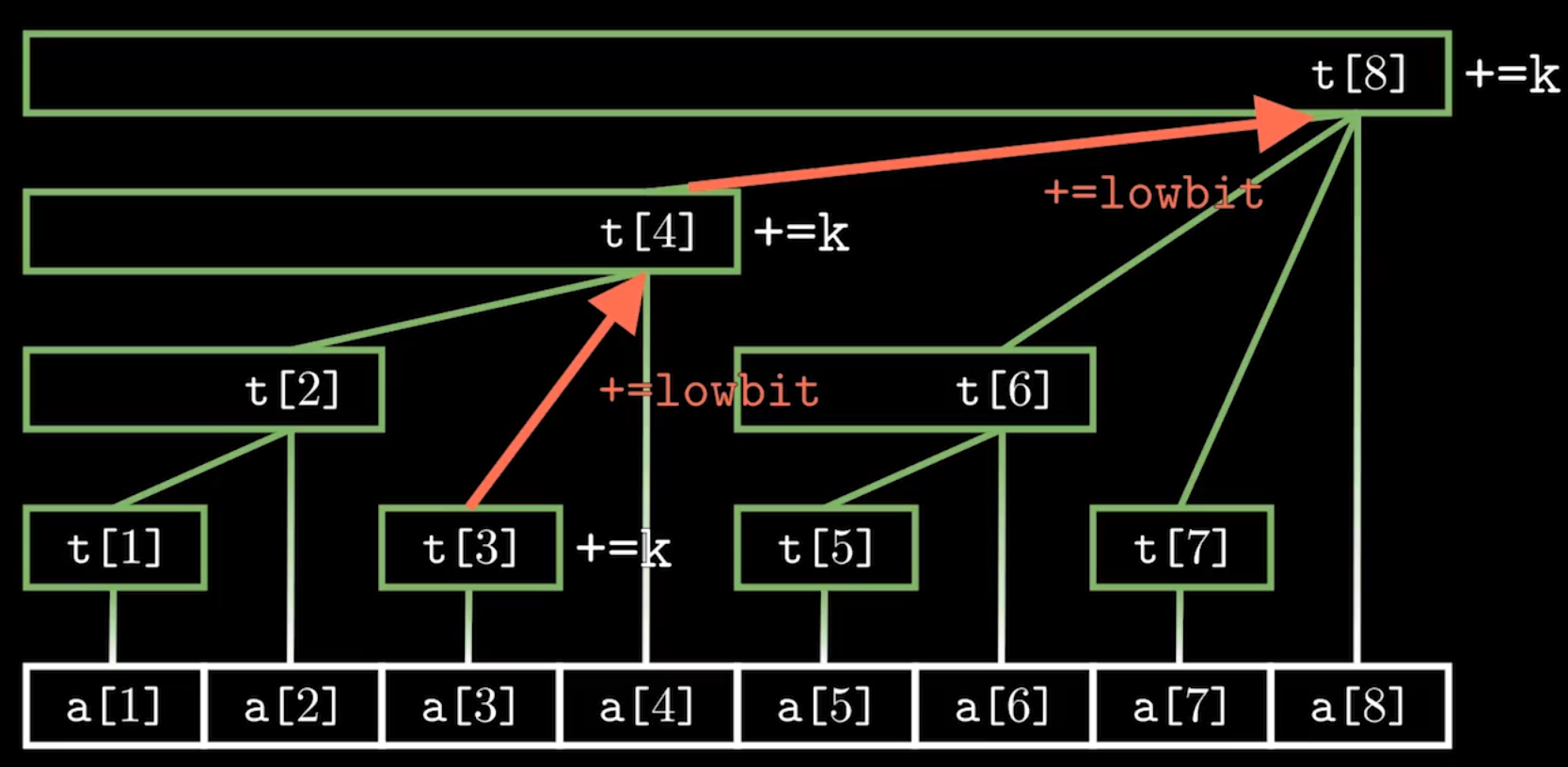
例如，更新 a[3]：

  1. 首先更新 t[3]。
  2. 下一个要更新的是 3 + lowbit(3) = 3 + 1 = 4，所以更新 t[4]。
  3. 再下一个是 4 + lowbit(4) = 4 + 4 = 8，所以更新 t[8]。
  4. 再下一个是 8 + lowbit(8) = 8 + 8 = 16，超出范围，停止。
    所以，更新 a[3] 会影响到 t[3], t[4], t[8]。这个过程的长度是 log n 级别的。

单点更新操作

前缀和查询 (query(index))

当你查询前缀和 Sum(1, i) 时，你需要把能拼凑成 [1, i] 区间的所有 t 元素加起来。

这些需要被累加的 t 元素形成了一条向下的路径。如何找到下一个要累加的节点？
规律是：i = i - lowbit(i)。

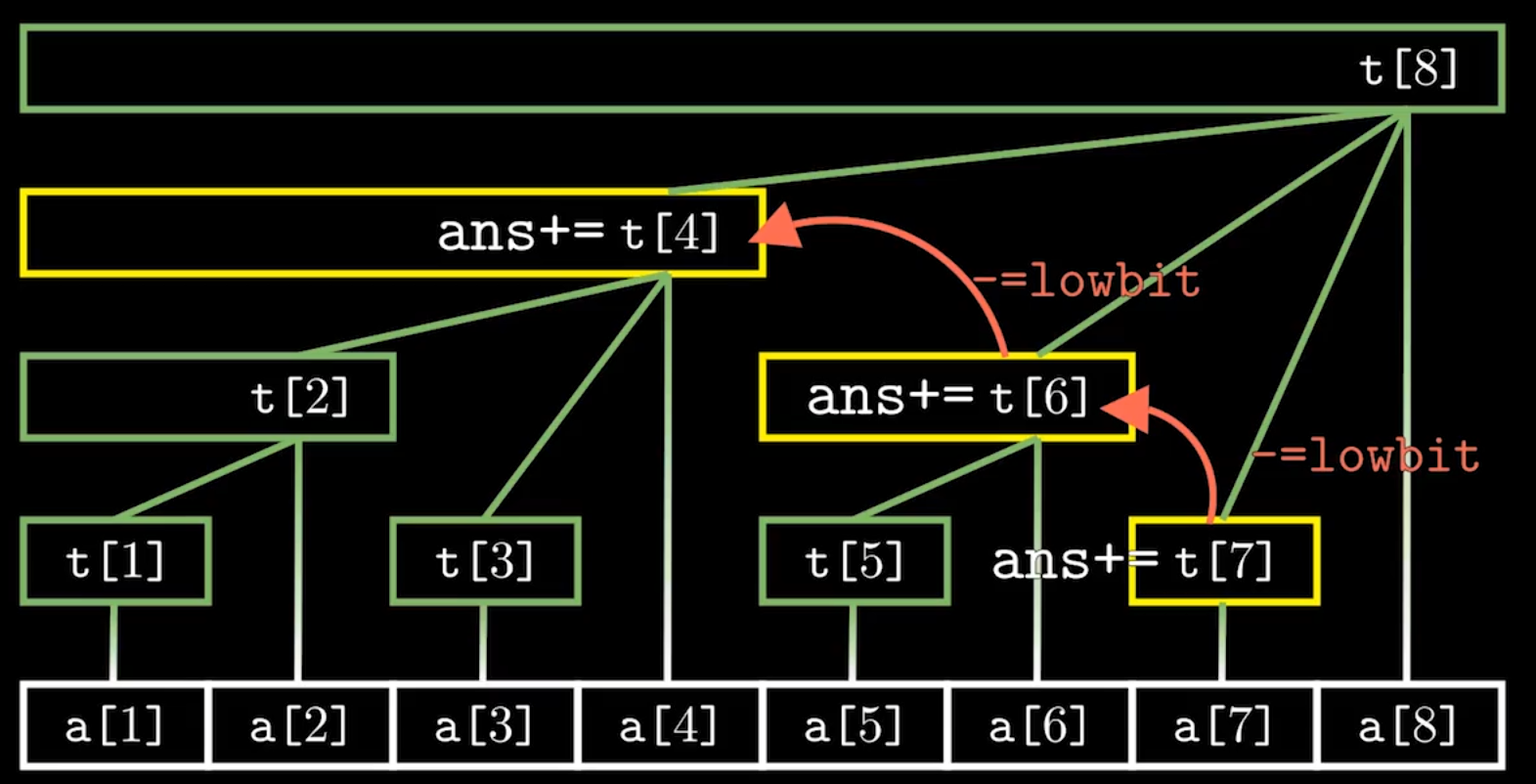
例如，查询前缀和 Sum(1, 7)：

  1. 首先加上 t[7] (管辖 a[7])。
  2. 下一个要加的是 7 - lowbit(7) = 7 - 1 = 6，所以加上 t[6] (管辖 a[5], a[6])。
  3. 再下一个是 6 - lowbit(6) = 6 - 2 = 4，所以加上 t[4] (管辖 a[1], a[2], a[3], a[4])。
  4. 再下一个是 4 - lowbit(4) = 4 - 4 = 0，停止。
    所以，Sum(1, 7) = t[7] + t[6] + t[4]。这个过程的长度也是 log n 级别的。

前缀和查询

3. Python 代码实现

为了方便，树状数组的实现通常采用 1-based 索引，即数组下标从 1 开始。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class FenwickTree:
    """
    树状数组 (Fenwick Tree / Binary Indexed Tree)
    支持单点更新和前缀和查询，时间复杂度均为 O(log n)
    """
    def __init__(self, size):
        """
        初始化一个大小为 size 的树状数组。
        通常 size 为原数组长度 n。内部数组大小为 n+1，使用 1-based 索引。
        """
        self.size = size
        self.tree = [0] * (size + 1)

    def _lowbit(self, x):
        """返回 x 的二进制表示中最低位的 1 所代表的值"""
        return x & (-x)

    def update(self, index, delta):
        """
        在原数组的 index 位置上增加 delta。
        index 是 1-based。
        """
        while index <= self.size:
            self.tree[index] += delta
            index += self._lowbit(index)

    def query(self, index):
        """
        查询原数组前缀 [1, index] 的和。
        index 是 1-based。
        """
        result = 0
        while index > 0:
            result += self.tree[index]
            index -= self._lowbit(index)
        return result

    def query_range(self, left, right):
        """
        查询原数组区间 [left, right] 的和。
        left 和 right 都是 1-based。
        """
        if left > right:
            return 0
        return self.query(right) - self.query(left - 1)

4. 经典应用场景

场景一：单点更新，区间查询 (最经典)

问题描述：给定一个数组，有两种操作：

  1. update i val: 将数组第 i 个元素的值改为 val。
  2. query l r: 查询区间 [l, r] 的和。

解法：
直接使用上面的模板。对于 update 操作，由于我们模板中的 update 是增加一个 delta，所以我们需要先知道原值，计算出差值 delta。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 假设我们有一个初始数组 nums
nums = [1, 3, 5, 7, 9, 11]
n = len(nums)

# 0. 为了方便，我们创建一个 1-based 的原数组副本
#    在实际应用中，如果只需要相对变化，可以不需要这个
original_array = [0] + nums 

# 1. 初始化树状数组
ft = FenwickTree(n)

# 2. 将初始数组的值填入树状数组
for i in range(1, n + 1):
    ft.update(i, original_array[i])

# 3. 执行查询操作
# 查询区间 [2, 5] 的和 (3 + 5 + 7 + 9)
print(f"Sum of range [2, 5]: {ft.query_range(2, 5)}")  # 输出 24

# 4. 执行更新操作
# 将第 3 个元素（值为5）更新为 6，即增加 1
index_to_update = 3
new_value = 6
delta = new_value - original_array[index_to_update]
ft.update(index_to_update, delta)
original_array[index_to_update] = new_value # 别忘了更新我们的副本

# 5. 再次查询
# 查询区间 [2, 5] 的和 (3 + 6 + 7 + 9)
print(f"Sum of range [2, 5] after update: {ft.query_range(2, 5)}") # 输出 25

场景二：区间更新，单点查询

问题描述：给定一个数组，有两种操作：

  1. update l r val: 将区间 [l, r] 内的每个元素都增加 val。
  2. query i: 查询第 i 个元素的值。

解法：
这需要一个巧妙的转换：差分数组。
我们维护原数组 a 的差分数组 D，其中 D[i] = a[i] - a[i-1] (规定 a[0] = 0)。

  • 区间更新的影响：当我们将 a 的 [l, r] 区间都加上 val 时，差分数组 D 会发生什么变化？

    • D[l] 变为 (a[l]+val) - a[l-1] = D[l] + val。所以 D[l] 增加了 val。
    • D[r+1] 变为 a[r+1] - (a[r]+val) = D[r+1] - val。所以 D[r+1] 减少了 val。
    • 对于 l 和 r+1 之间的 i，D[i] 不变。
      所以，一个区间更新 [l, r] 被转换成了两个单点更新 D[l] 和 D[r+1]。

  • 单点查询的计算：原数组的 a[i] 值等于其差分数组的前缀和。
    a[i] = D[1] + D[2] + ... + D[i]。

综上，我们可以在差分数组 D 上建立一个树状数组，从而实现：

  • 区间更新 -> O(log n) (两次单点更新)
  • 单点查询 -> O(log n) (一次前缀和查询)

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 假设初始数组全为 0，大小为 n
n = 10
# 我们在差分数组上建立树状数组
# 差分数组初始也全为 0
diff_ft = FenwickTree(n) 

# 操作1: 区间 [2, 7] 增加 5
l, r, val = 2, 7, 5
diff_ft.update(l, val)
if r + 1 <= n:
    diff_ft.update(r + 1, -val)

# 操作2: 区间 [4, 9] 增加 2
l, r, val = 4, 9, 2
diff_ft.update(l, val)
if r + 1 <= n:
    diff_ft.update(r + 1, -val)

# 操作3: 查询第 5 个元素的值
# a[5] = D[1] + D[2] + ... + D[5]
index_to_query = 5
value = diff_ft.query(index_to_query)
print(f"Value at index {index_to_query}: {value}") # 应该输出 7 (5+2)

# 操作4: 查询第 8 个元素的值
index_to_query = 8
value = diff_ft.query(index_to_query)
print(f"Value at index {index_to_query}: {value}") # 应该输出 2

场景三：区间更新，区间查询

问题描述：给定一个数组，有两种操作：

  1. update l r val: 将区间 [l, r] 内的每个元素都增加 val。
  2. query l r: 查询区间 [l, r] 的和。

解法：
这是最复杂的场景，需要两个树状数组。
基于场景二的差分思想，我们要求 Sum(a[1]...a[x])。
Sum(a[1]..a[x]) = Sum_{i=1 to x} a[i] = Sum_{i=1 to x} Sum_{j=1 to i} D[j]
这个公式可以进行数学推导和展开：
Sum_{i=1 to x} (x - i + 1) * D[i]
= (x+1) * Sum_{i=1 to x} D[i] - Sum_{i=1 to x} i * D[i]

这个公式告诉我们，为了求 a 的前缀和，我们需要维护两个东西：

  1. Sum_{i=1 to x} D[i]
  2. Sum_{i=1 to x} i * D[i]

因此，我们建立两个树状数组：

  • BIT1：维护差分数组 D。
  • BIT2：维护 i * D[i] 构成的数组。

操作流程：

  • 区间更新 [l, r] 加 val：
    • 在 BIT1 上：update(l, val), update(r+1, -val)。
    • 在 BIT2 上：update(l, l*val), update(r+1, -(r+1)*val)。
  • 查询前缀和 Sum(a[1]..a[x])：
    • 结果 = (x+1) * BIT1.query(x) - BIT2.query(x)。
  • 查询区间和 Sum(a[l]..a[r])：
    • 结果 = prefix_sum(r) - prefix_sum(l-1)。

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class AdvancedFenwickTree:
    def __init__(self, size):
        self.size = size
        self.bit1 = FenwickTree(size) # 维护 D[i]
        self.bit2 = FenwickTree(size) # 维护 i * D[i]

    def update_range(self, left, right, delta):
        # 对 BIT1 更新
        self.bit1.update(left, delta)
        self.bit1.update(right + 1, -delta)
        # 对 BIT2 更新
        self.bit2.update(left, left * delta)
        self.bit2.update(right + 1, (right + 1) * (-delta))

    def _query_prefix_sum(self, index):
        # 根据公式计算 a 的前缀和
        res1 = self.bit1.query(index)
        res2 = self.bit2.query(index)
        return (index + 1) * res1 - res2

    def query_range_sum(self, left, right):
        # 区间和 = 前缀和之差
        sum_right = self._query_prefix_sum(right)
        sum_left_minus_1 = self._query_prefix_sum(left - 1)
        return sum_right - sum_left_minus_1

# 示例
n = 10
adv_ft = AdvancedFenwickTree(n)

# 初始数组全为 0
# 区间 [2, 7] 增加 3
adv_ft.update_range(2, 7, 3)

# 区间 [4, 9] 增加 5
adv_ft.update_range(4, 9, 5)

# 查询区间 [3, 8] 的和
# a[3] = 3
# a[4] = 3+5=8
# a[5] = 3+5=8
# a[6] = 3+5=8
# a[7] = 3+5=8
# a[8] = 5
# Sum = 3 + 8*4 + 5 = 3 + 32 + 5 = 40
print(f"Sum of range [3, 8]: {adv_ft.query_range_sum(3, 8)}") # 输出 40

参考

[1] 〔manim | 算法 | 数据结构〕 完全理解并深入应用树状数组 | 支持多种动态维护区间操作