二分查找 | 星海流光

二分法是一种较为简单通用的搜索算法，但是在实际动手写时，却经常因为细节问题导致无法一次性写对，这里整理出了现代二分法的最佳实践写法，即红蓝染色/边界搜索算法，理解该方法后对于各种二分变种问题都能一次写对。

红蓝染色/边界搜索算法

"""
题目描述：
给定数组nums = [1, 3, 6, 6, 6, 12, 16, 19, 20]

target = 6
若数组中包含target，则返回数组下标，否则返回-1
"""
# 采用红蓝染色/边界查找法，现代二分法的最佳实践
def binary_search_lower_bound(nums, target):
    """lower_bound问题的二分搜索写法"""
    left, right = -1, len(nums)

    while left + 1 != right:
        middle = left + (right - left) // 2
        # 如果middle指针在蓝色区域
        if nums[middle] < target:
            left = middle
        else:
            right = middle
    # 可自己根据实际问题返回左指针或右指针
    return right

def binary_search_upper_bound(nums, target):
    """upper_bound问题的二分搜索写法"""
    left, right = -1, len(nums)

    while left + 1 != right:
        middle = left + (right - left) // 2
        # 如果middle指针在蓝色区域
        if nums[middle] <= target:
            left = middle
        else:
            right = middle
    # 可自己根据实际问题返回左指针或右指针
    return right


if __name__ == "__main__":
    nums = [1, 3, 6, 6, 6, 12, 16, 19, 20]
    target = 6
    # 注意使用二分法的前提是数组必须是有序的
    nums.sort()

    # # 检查索引是否越界，以及该位置的元素是否等于target
    # if index < len(nums) and nums[index] == target:
    #     return index  # 找到了，返回索引
    # else:
    #     return -1  # 未找到
    print(binary_search_lower_bound(nums, target))
    print(binary_search_upper_bound(nums, target))

"""
输出结果为：
2
5
"""

C++20 std::ranges 中的 lower_bound、upper_bound 与 Python bisect 模块中的 bisect_left、bisect_right，这四个函数本质上都做同一件事：在一个已排序的序列中，使用二分查找算法来高效地找到一个合适的位置。它们的核心目的不是简单地“查找”一个元素是否存在，而是确定一个值应该被插入到序列的哪个位置，才能继续保持序列的有序性。

核心概念理解

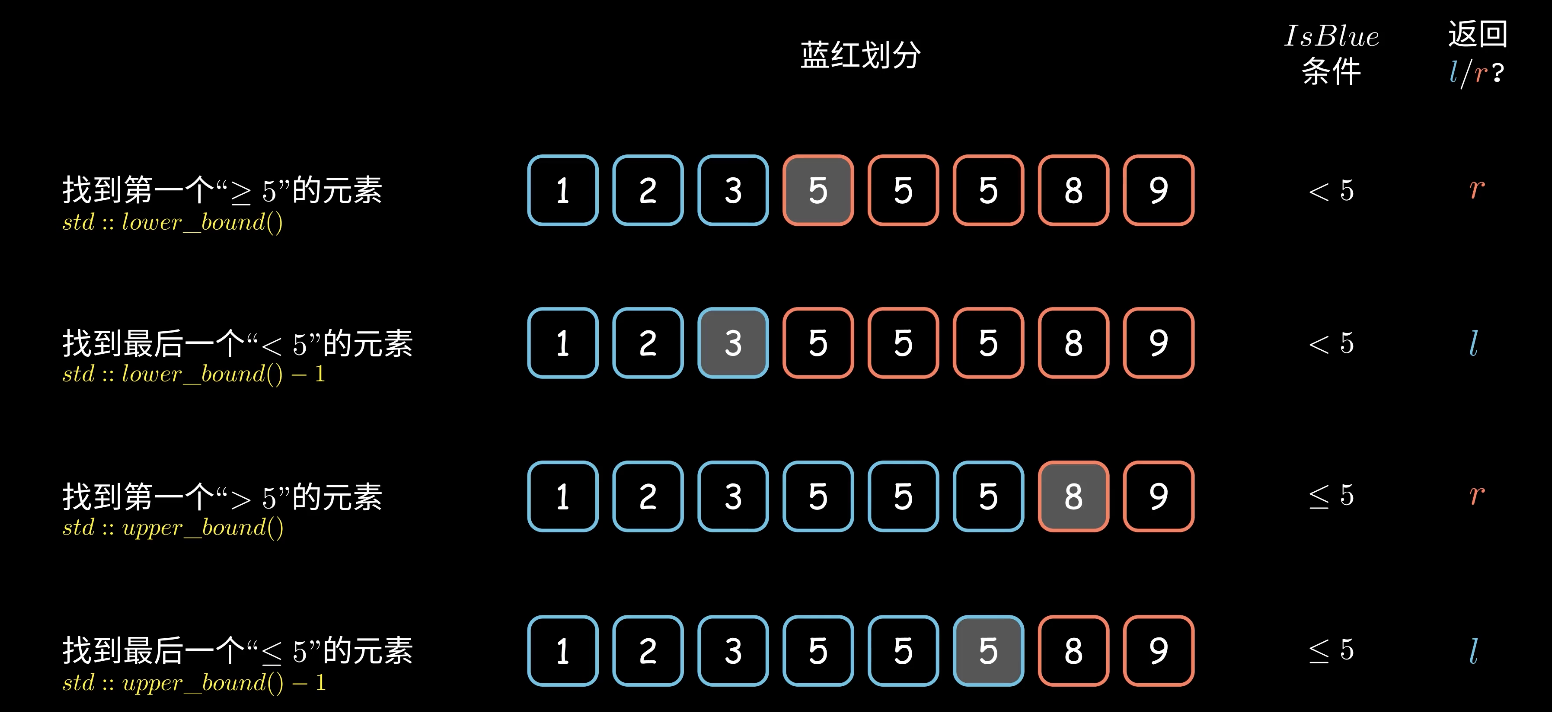
在深入细节之前，我们先统一理解两个核心概念：lower_bound（或 left）和 upper_bound（或 right）。

假设你有一个已排序的序列，比如 [10, 20, 30, 30, 30, 40, 50]，现在你想查找值 30。

lower_bound / bisect_left (寻找下界/左边界)
- 它会找到序列中第一个可以插入 30 而不破坏排序的位置。
- 换句话说，它返回的是第一个不小于（大于或等于）30 的元素的位置。
- 在 [10, 20, **30**, 30, 30, 40, 50] 中，这个位置是第一个 30 所在的位置（索引 2）。
upper_bound / bisect_right (寻找上界/右边界)
- 它会找到序列中最后一个可以插入 30 而不破坏排序的位置。
- 换句话说，它返回的是第一个严格大于30 的元素的位置。
- 在 [10, 20, 30, 30, 30, **40**, 50] 中，这个位置是 40 所在的位置（索引 5）。

一个关键的记忆技巧：

_left / lower_ 会把新元素插入到现有相同元素的左边。
_right / upper_ 会把新元素插入到现有相同元素的右边。

第一部分：C++ `std::ranges::lower_bound` 和 `std::ranges::upper_bound`

这些是 C++20 ranges 库的一部分，相比于 C++17 及之前的 std::lower_bound，它们提供了更现代化、更简洁的接口。

前提条件：操作的范围（range）必须已经根据所用的比较操作排好序。

返回值：返回一个迭代器（iterator），指向找到的位置。如果找不到符合条件的位置（例如，查找的值比所有元素都大），则返回范围的 end() 迭代器。

1. `std::ranges::lower_bound`

签名 (简化版):

1
2
3

template<forward_range R, class T, class Proj = identity, class Comp = ranges::less>
constexpr borrowed_iterator_t<R>
    lower_bound(R&& r, const T& value, Comp comp = {}, Proj proj = {});

R&& r: 一个范围，例如 std::vector、std::array 或 std::string_view。
const T& value: 要查找的值。
Comp comp (可选): 自定义比较函数对象。默认是 std::ranges::less，即 < 运算符。
Proj proj (可选): 投影函数。在比较之前，会对范围中的每个元素应用这个函数。这是一个非常强大的功能。

详细解释：
它返回一个迭代器 it，指向范围 r 中第一个满足 !comp(proj(*it), value) 的元素。
如果使用默认的 comp (<) 和 proj (无操作)，这个条件就等价于 !(*it < value)，也就是 *it >= value。

代码示例：

#include <iostream>
#include <vector>
#include <ranges>
#include <algorithm>

void print_pos(const std::string& func_name, const std::vector<int>& vec, std::vector<int>::iterator it) {
    std::cout << func_name << ": ";
    if (it == vec.end()) {
        std::cout << "Element should be inserted at the end (index " << vec.size() << ")\n";
    } else {
        auto index = std::distance(vec.begin(), it);
        std::cout << "Found at index " << index << ", value is " << *it << "\n";
    }
}

int main() {
    std::vector<int> v = {10, 20, 30, 30, 30, 40, 50};

    // 1. 查找一个存在且重复的元素
    std::cout << "Searching for 30:\n";
    auto it_lower = std::ranges::lower_bound(v, 30);
    print_pos("lower_bound", v, it_lower); // 指向第一个 30 (索引 2)

    // 2. 查找一个不存在的元素
    std::cout << "\nSearching for 25:\n";
    it_lower = std::ranges::lower_bound(v, 25);
    print_pos("lower_bound", v, it_lower); // 指向第一个 30 (索引 2)，因为 30 是第一个 >= 25 的元素

    // 3. 查找一个比所有元素都大的元素
    std::cout << "\nSearching for 60:\n";
    it_lower = std::ranges::lower_bound(v, 60);
    print_pos("lower_bound", v, it_lower); // 指向 end()

    // 4. 查找一个比所有元素都小的元素
    std::cout << "\nSearching for 5:\n";
    it_lower = std::ranges::lower_bound(v, 5);
    print_pos("lower_bound", v, it_lower); // 指向第一个元素 10 (索引 0)
}

2. `std::ranges::upper_bound`

签名 (与 lower_bound 类似):

1
2
3

template<forward_range R, class T, class Proj = identity, class Comp = ranges::less>
constexpr borrowed_iterator_t<R>
    upper_bound(R&& r, const T& value, Comp comp = {}, Proj proj = {});

详细解释：
它返回一个迭代器 it，指向范围 r 中第一个满足 comp(value, proj(*it)) 的元素。
如果使用默认的 comp 和 proj，这个条件就等价于 value < *it，也就是 *it > value。

代码示例 (续上):

#include <iostream>
#include <vector>
#include <ranges>
#include <algorithm>

// ... print_pos function from above ...

int main() {
    std::vector<int> v = {10, 20, 30, 30, 30, 40, 50};

    // 1. 查找一个存在且重复的元素
    std::cout << "Searching for 30:\n";
    auto it_upper = std::ranges::upper_bound(v, 30);
    print_pos("upper_bound", v, it_upper); // 指向 40 (索引 5)，因为 40 是第一个 > 30 的元素

    // 2. 查找一个不存在的元素
    std::cout << "\nSearching for 25:\n";
    it_upper = std::ranges::upper_bound(v, 25);
    print_pos("upper_bound", v, it_upper); // 指向第一个 30 (索引 2)，因为 30 是第一个 > 25 的元素

    // 3. 查找一个比所有元素都大的元素
    std::cout << "\nSearching for 60:\n";
    it_upper = std::ranges::upper_bound(v, 60);
    print_pos("upper_bound", v, it_upper); // 指向 end()

    // 4. 查找一个比所有元素都小的元素
    std::cout << "\nSearching for 5:\n";
    it_upper = std::ranges::upper_bound(v, 5);
    print_pos("upper_bound", v, it_upper); // 指向第一个元素 10 (索引 0)
}

C++ 投影 (Projection) 的强大之处

假设你有一个结构体 Person 的 vector，并按年龄排序，你想查找特定年龄的人。

struct Person {
    std::string name;
    int age;
};

int main() {
    std::vector<Person> people = {{"Alice", 20}, {"Bob", 25}, {"Charlie", 25}, {"David", 30}};
    // 按年龄排序
    // std::ranges::sort(people, {}, &Person::age); // 假设已经排序

    int age_to_find = 25;

    // 使用投影来直接在 Person vector 中查找年龄
    auto it = std::ranges::lower_bound(people, age_to_find, {}, &Person::age);

    if (it != people.end()) {
        std::cout << "First person with age >= 25 is " << it->name << " at age " << it->age << std::endl;
    }
}

这里，&Person::age 是一个投影，它告诉 lower_bound：“在比较时，不要看整个 Person 对象，只看它的 age 成员。” 这使得代码非常干净和直观。

第二部分：Python `bisect.bisect_left` 和 `bisect.bisect_right`

这些函数位于 Python 标准库的 bisect 模块中。

前提条件：操作的列表（list）必须已经排好序。

返回值：返回一个整数索引（index），表示合适的插入点。这与 C++ 返回迭代器是主要区别之一。

1. `bisect.bisect_left`

签名:

1	bisect.bisect_left(a, x, lo=0, hi=len(a))

a: 已排序的序列（通常是列表）。
x: 要查找的值。
lo, hi (可选): 指定在序列的哪个子切片中进行搜索。

详细解释：
功能上完全等同于 C++ 的 lower_bound。它返回一个插入点 i，这个插入点会将 x 插入到 a 中所有等于 x 的元素之前。

代码示例：

import bisect

a = [10, 20, 30, 30, 30, 40, 50]

# 1. 查找一个存在且重复的元素
print("Searching for 30:")
idx_left = bisect.bisect_left(a, 30)
print(f"bisect_left: index is {idx_left}") # 输出 index is 2

# 2. 查找一个不存在的元素
print("\nSearching for 25:")
idx_left = bisect.bisect_left(a, 25)
print(f"bisect_left: index is {idx_left}") # 输出 index is 2 (25应该插入到30之前)

# 3. 查找一个比所有元素都大的元素
print("\nSearching for 60:")
idx_left = bisect.bisect_left(a, 60)
print(f"bisect_left: index is {idx_left}") # 输出 index is 7 (列表长度)

# 4. 查找一个比所有元素都小的元素
print("\nSearching for 5:")
idx_left = bisect.bisect_left(a, 5)
print(f"bisect_left: index is {idx_left}") # 输出 index is 0

2. `bisect.bisect_right`

签名 (与 bisect_left 类似):

1	bisect.bisect_right(a, x, lo=0, hi=len(a))

bisect.bisect 是 bisect.bisect_right 的一个别名，两者完全相同。

详细解释：
功能上完全等同于 C++ 的 upper_bound。它返回一个插入点 i，这个插入点会将 x 插入到 a 中所有等于 x 的元素之后。

代码示例 (续上):

import bisect

a = [10, 20, 30, 30, 30, 40, 50]

# 1. 查找一个存在且重复的元素
print("Searching for 30:")
idx_right = bisect.bisect_right(a, 30)
print(f"bisect_right: index is {idx_right}") # 输出 index is 5

# 2. 查找一个不存在的元素
print("\nSearching for 25:")
idx_right = bisect.bisect_right(a, 25)
print(f"bisect_right: index is {idx_right}") # 输出 index is 2 (和 bisect_left 结果相同)

# 3. 查找一个比所有元素都大的元素
print("\nSearching for 60:")
idx_right = bisect.bisect_right(a, 60)
print(f"bisect_right: index is {idx_right}") # 输出 index is 7

# 4. 查找一个比所有元素都小的元素
print("\nSearching for 5:")
idx_right = bisect.bisect_right(a, 5)
print(f"bisect_right: index is {idx_right}") # 输出 index is 0

注意：Python 的 bisect 模块本身没有 C++ ranges 那样直接的 key 或 projection 参数。如果你需要对复杂对象列表进行操作，通常有两种方法：

创建一个只包含用于排序的键的临时列表，然后用 bisect 操作这个键列表。
将你的对象封装在一个类中，并实现 __lt__ 等比较方法，这样 bisect 就可以直接比较对象了。
从 Python 3.10 开始，bisect 函数新增了 key 参数，用法和 sorted() 的 key 类似，这使得它和 C++ 的投影功能对齐了。

核心差异与总结

特性	C++ `std::ranges`	Python `bisect`
核心功能	查找排序序列中的插入点	查找排序序列中的插入点
`lower_bound`/`_left`	返回第一个不小于目标值的位置	返回第一个不小于目标值的位置
`upper_bound`/`_right`	返回第一个严格大于目标值的位置	返回第一个严格大于目标值的位置
返回值类型	迭代器 (Iterator)	整数索引 (Integer Index)
库/模块	C++20 `<ranges>` 标准库	Python `bisect` 标准库模块
处理复杂对象	非常强大，通过投影(projection)和自定义比较(comparator)实现	Python 3.10+ 支持 `key` 参数。之前版本需要额外处理。
语法	`std::ranges::func(range, value, comp, proj)`	`bisect.func(list, value, lo, hi, key)`

常见应用场景

这些函数非常有用，远不止查找那么简单。

1. 高效地保持列表/向量有序

这是它们的本职工作。

Python:
1
a.insert(bisect.bisect_left(a, x), x)

C++:

1	v.insert(std::ranges::lower_bound(v, x), x);

2. 计算有序序列中特定值的数量

这是一个非常经典的用法。等于 value 的所有元素构成一个连续的区间，其起始点由 lower_bound 给出，结束点（不包含）由 upper_bound 给出。

Python:

1 2	count = bisect.bisect_right(a, 30) - bisect.bisect_left(a, 30) # count = 5 - 2 = 3

C++:

1
2
3

auto count = std::distance(std::ranges::lower_bound(v, 30),
                           std::ranges::upper_bound(v, 30));
// count = 3

3. 检查元素是否存在

虽然有更直接的方法（如 std::ranges::binary_search 或 Python 的 in），但也可以用 lower_bound 来实现，这在某些复杂逻辑中可能更方便。

Python:

1
2
3

i = bisect.bisect_left(a, x)
if i != len(a) and a[i] == x:
    print(f"{x} is in the list")

C++:

auto it = std::ranges::lower_bound(v, x);
if (it != v.end() && *it == x) {
    std::cout << x << " is in the vector" << std::endl;
}

这里必须检查 it != v.end()，因为如果 x 比所有元素都大，lower_bound 会返回 end()，解引用 end() 是未定义行为。

[1] 二分查找为什么总是写错？

核心概念理解

第一部分：C++ std::ranges::lower_bound 和 std::ranges::upper_bound

1. std::ranges::lower_bound

2. std::ranges::upper_bound

C++ 投影 (Projection) 的强大之处

第二部分：Python bisect.bisect_left 和 bisect.bisect_right

1. bisect.bisect_left

2. bisect.bisect_right

核心差异与总结

常见应用场景

1. 高效地保持列表/向量有序

2. 计算有序序列中特定值的数量

3. 检查元素是否存在

第一部分：C++ `std::ranges::lower_bound` 和 `std::ranges::upper_bound`

1. `std::ranges::lower_bound`

2. `std::ranges::upper_bound`

第二部分：Python `bisect.bisect_left` 和 `bisect.bisect_right`

1. `bisect.bisect_left`

2. `bisect.bisect_right`