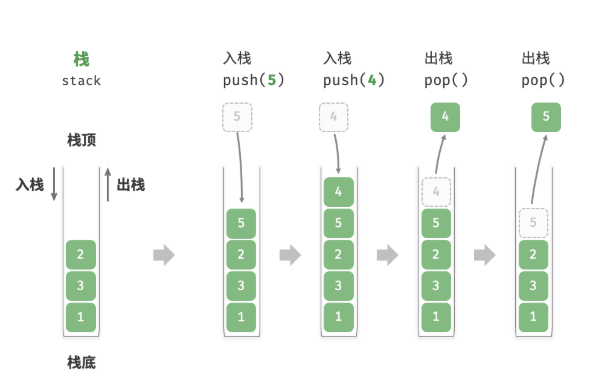
1. 栈的常用操作

栈的常用操作如下表所示：

方法	描述	时间复杂度
push()	元素入栈（添加至栈顶）	$O(1)$
pop()	栈顶元素出栈	$O(1)$
peek()	访问栈顶元素	$O(1)$

通常情况下，一些编程语言内置了栈类。当没有提供栈类时，可以将该语言的“数组”或“链表”当作栈来使用，并在程序逻辑上忽略与栈无关的操作。C++具有栈类stack可以直接使用，而Python的列表也有能轻易实现栈操作的方法，因此下面以C为例实现栈。

2. 栈的实现

栈可以视为一种受限制的数组或链表，因为它只能在栈顶添加或删除元素。换句话说，我们可以通过屏蔽数组或链表的部分无关操作，使其对外表现的逻辑符合栈的特性。

2.1 基于链表的实现

使用链表实现栈时，可以将链表的头节点视为栈顶，尾节点视为栈底。对于入栈操作，只需将元素插入链表头部，这种节点插入方法被称为“头插法”。而对于出栈操作，只需将头节点从链表中删除即可。

/* 基于链表实现的栈 */
typedef struct {
    ListNode *top; // 将头节点作为栈顶
    int size;      // 栈的长度
} LinkedListStack;

/* 构造函数 */
LinkedListStack *newLinkedListStack() {
    LinkedListStack *s = malloc(sizeof(LinkedListStack));
    s->top = NULL;
    s->size = 0;
    return s;
}

/* 析构函数 */
void delLinkedListStack(LinkedListStack *s) {
    while (s->top) {
        ListNode *n = s->top->next;
        free(s->top);
        s->top = n;
    }
    free(s);
}

/* 获取栈的长度 */
int size(LinkedListStack *s) {
    return s->size;
}

/* 判断栈是否为空 */
bool isEmpty(LinkedListStack *s) {
    return size(s) == 0;
}

/* 入栈 */
void push(LinkedListStack *s, int num) {
    ListNode *node = (ListNode *)malloc(sizeof(ListNode));
    node->next = s->top; // 更新新加节点指针域
    node->val = num;     // 更新新加节点数据域
    s->top = node;       // 更新栈顶
    s->size++;           // 更新栈大小
}

/* 访问栈顶元素 */
int peek(LinkedListStack *s) {
    if (s->size == 0) {
        printf("栈为空\n");
        return INT_MAX;
    }
    return s->top->val;
}

/* 出栈 */
int pop(LinkedListStack *s) {
    int val = peek(s);
    ListNode *tmp = s->top;
    s->top = s->top->next;
    // 释放内存
    free(tmp);
    s->size--;
    return val;
}

2.2 基于数组的实现

在使用数组实现栈时，我们可以将数组的尾部视为栈顶。入栈与出栈操作分别对应在数组尾部添加元素与删除变量，时间复杂度都为$O(1)$。

由于入栈的元素可能会源源不断地增加，因此我们可以使用动态数组，这样就无需自行处理数组扩容问题。

/* 基于数组实现的栈 */
typedef struct {
    int *data;
    int size;
} ArrayStack;

/* 构造函数 */
ArrayStack *newArrayStack() {
    ArrayStack *stack = malloc(sizeof(ArrayStack));
    // 初始化一个大容量，避免扩容
    stack->data = malloc(sizeof(int) * MAX_SIZE);
    stack->size = 0;
    return stack;
}

/* 析构函数 */
void delArrayStack(ArrayStack *stack) {
    free(stack->data);
    free(stack);
}

/* 获取栈的长度 */
int size(ArrayStack *stack) {
    return stack->size;
}

/* 判断栈是否为空 */
bool isEmpty(ArrayStack *stack) {
    return stack->size == 0;
}

/* 入栈 */
void push(ArrayStack *stack, int num) {
    if (stack->size == MAX_SIZE) {
        printf("栈已满\n");
        return;
    }
    stack->data[stack->size] = num;
    stack->size++;
}

/* 访问栈顶元素 */
int peek(ArrayStack *stack) {
    if (stack->size == 0) {
        printf("栈为空\n");
        return INT_MAX;
    }
    return stack->data[stack->size - 1];
}

/* 出栈 */
int pop(ArrayStack *stack) {
    int val = peek(stack);
    stack->size--;
    return val;
}